
Born:- 27 December 1571
Died:- 15 November 1630 (aged 58)
Johannes Kepler, a German astronomer, mathematician, astrologer, natural philosopher, and music composer, was born on December 27, 1571, and died on November 15, 1630. His laws of planetary motion and the books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, which influenced Isaac Newton and laid the groundwork for his theory of universal gravitation, make him a pivotal figure in the 17th-century Scientific Revolution. Kepler is regarded as one of the founding fathers of modern astronomy, the scientific method, natural science, and contemporary science due to the breadth and significance of his contributions. Because of his book Somnium, he has been referred to be the “father of science fiction”.
While teaching mathematics at a seminary school in Graz, Kepler got to know Prince Hans Ulrich von Eggenberg. He finally rose to the position of imperial mathematician under Emperor Rudolf II and his two successors, Matthias and Ferdinand II, after serving as Tycho Brahe’s assistant in Prague. at addition, he served as General Wallenstein’s advisor while teaching mathematics at Linz. He also accomplished important work in the science of optics, earning the title of “father of modern optics” according to his Astronomiae pars optical.
Along with improving on Galileo Galilei’s telescope design—who acknowledged Kepler’s discoveries in his work—he also created an upgraded refracting telescope known as the Keplerian telescope, which laid the groundwork for the contemporary refracting telescope.
Kepler lived in a time when astrology and astronomy were not clearly distinguished, but astronomy—a part of mathematics under the liberal arts—and physics—a branch of natural philosophy—were sharply divided. Motivated by the religious conviction and belief that God had created the universe according to an understandable design that is accessible through the natural light of reason, Kepler also included religious reasons and reasoning into his work. The old tradition of physical cosmology was transformed by Kepler’s new astronomy, which he referred to as “celestial physics,” “an excursion into Aristotle’s Metaphysics,” and “a supplement to Aristotle’s On the Heavens.” Astronomy was treated as a component of a universal mathematical physics.
Early Years
Childhood (1571–1590)
Kepler was born on December 27, 1571, in Weil der Stadt, a Free Imperial City in the German state of Baden-Württemberg. Today, Weil der Stadt is a part of the Stuttgart Region. Sebald Kepler, his grandfather, had served as the city’s Lord Mayor. The Kepler family’s riches was fading by the time Johannes was born. When Johannes was five years old, his father Heinrich Kepler, a mercenary, abandoned the family to make a little income. It was thought that he perished in the Netherlands during the Eighty Years’ War. His mother, Katharina Guldenmann, was a herbalist and healer. She was the daughter of an innkeeper.
Two brothers and one sister out of Johannes’s six siblings lived to maturity. He claimed to have been frail and ill as a youngster due to his preterm birth. Nevertheless, his extraordinary mathematical ability frequently astounded guests at his grandfather’s inn.
He was first exposed to astronomy at a young age, and he would grow to have a lifelong fascination for it. Having seen the Great Comet of 1577 at the age of six, he wrote that he “was taken by [his] mother to a high place to look at it.” When he saw a lunar eclipse in 1580, at the age of nine, he noted that he had been “called outdoors” to witness it and that the Moon “appeared quite red.” Nevertheless, the smallpox he contracted as a youngster left him with impaired hands and weak vision, which limited his capacity for astronomical observation.

Following his time at Maulbronn’s grammar school, Latin school, and seminary, Kepler enrolled at Tübinger Stift at the University of Tübingen in 1589. Before becoming Chancellor of Tübingen in 1590, he studied philosophy under Vitus Müller and theology under Jacob Heerbrand, a pupil of Philipp Melanchthon at Wittenberg, who also instructed Michael Maestlin.
He demonstrated his exceptional mathematical abilities and gained recognition as a proficient astrologer by interpreting horoscopes for his fellow classmates. He studied the Copernican and Ptolemaic systems of planetary motion with Michael Maestlin, the mathematics professor at Tübingen from 1583 to 1631. At that point, he turned Copernican. He supported heliocentrism in a student dispute, arguing that the Sun was the universe’s primary source of motive force from both a theoretical and religious standpoint. He wanted to be a Lutheran preacher, but his views ran counter to the Formula of Concord, thus he was not allowed to be ordained.
At the close of his studies, Kepler received a recommendation to become an astronomy and mathematics teacher at the Protestant school in Graz. At the age of 22, he accepted the office in April of 1594.
Graz (1594–1600)
Kepler took an opportunity to replace Georg Stadius as a math teacher at the Protestant school in Graz (now in Styria, Austria) prior to finishing his studies at Tübingen. He published several official calendars and predictions during this time (1594–1600), which improved his standing as an astrologer. Kepler was not a great fan of astrology and disapproved of many of the customs of astrologers, but he did believe that there was a relationship between the individual and the universe. A little more than a year after arriving in Graz, in 1596, he published some of the ideas he had entertained while still a student in the Mysterium Cosmographicum.
Kepler started pursuing Barbara Müller in December 1595 after learning about her. Müller was a 23-year-old widow (twice over) with a little daughter named Regina Lorenz. Müller was the daughter of a prosperous mill owner and an heir to the estates of her late husbands. At first, her father Jobst was against marriage.
Kepler was an undesirable match despite having inherited his grandfather’s nobility due to his poverty. After Kepler finished work on Mysterium, Jobst gave in, but the engagement almost fell apart while Kepler was away taking care of publishing-related matters. Protestant authorities, who had assisted in arranging the match, put pressure on the Müllers to stick to their arrangement, nevertheless. April 27, 1597, saw the marriage of Barbara and Johannes.
The Keplers lost both of their infant children, Heinrich and Susanna, during the early years of their marriage. They had three children: a girl named Susanna in 1602, a boy named Friedrich in 1604, and another son named Ludwig in 1607.
Additional study

With the approval of the Graz school inspectors and after Mysterium was published, Kepler embarked on an ambitious mission to expand and refine his work. He intended to write four more books: one about the motions of the planets, one about the stationary aspects of the universe (the Sun and fixed stars), one about the physical makeup of the planets and the formation of geographical features (mostly on Earth), and one about the effects of the heavens on Earth, encompassing atmospheric optics, meteorology, and astrology.
He also wanted the views of several of the astronomers he had given Mysterium to, including Reimarus Ursus (Nicolaus Reimers Bär), Rudolf II’s imperial mathematician and Tycho Brahe’s fiercest opponent. Instead of explicitly responding, Ursus publicized Kepler’s kind letter in order to press Tycho’s priority dispute over the Tychonic system. Despite this black mark, Tycho also started writing to Kepler, offering a severe but valid criticism of Kepler’s method, pointing out among many other things that the use of erroneous numerical data from Copernicus was one of his many grievances.

Tycho and Kepler exchanged communications on a wide variety of astronomical issues, focusing in particular on moon occurrences and the theological feasibility of Copernican doctrine.
However, Kepler was unable to resolve many of these problems in the absence of Tycho’s observatory’s far more precise data.

Rather, he focused on the astrological implications of chronology and “harmony,” the numerological connections between mathematics, music, and the physical universe. Presuming that the Earth had a soul (a quality he would later invoke to explain why the Sun drives planets into motion), he developed a theoretical framework that linked astrological features and astronomical distances to weather and other terrestrial occurrences. But by 1599, he was once more constrained in his work by the imprecision of the information at hand—just as mounting religious unrest was posing a danger to his job in Graz.
Tycho requested Kepler to visit him in Prague in December of that year; Kepler left on January 1, 1600, even before receiving the invitation, hoping that Tycho’s sponsorship would help him with both his philosophical and his social and economical issues.
A Career in Science
Prague between 1600 and 1612

Kepler first met Tycho Brahe and his colleagues, Franz Tengnagel and Longomontanus, on February 4, 1600, in Benátky nad Jizerou, which is 35 km from Prague. Tycho was building a new observatory at this location. He stayed as a guest for the following two months, studying some of Tycho’s observations of Mars. Tycho was first reluctant to give Kepler additional access, but he was eventually won over by his theoretical ideas. Kepler anticipated that the task (because he was not permitted to simply copy the data for his personal use) would take up to two years in order to prove his theory from Mysterium Cosmographicum based on the Mars data.
Kepler tried, with Johannes Jessenius’s assistance, to talk Tycho into a more formal work contract, but the talks ended in a furious dispute, and on April 6th, Kepler departed for Prague. After a brief period of reconciliation and an agreement on wage and living conditions, Kepler went back to Graz in June to pick up his family.
His plans to return right once to Brahe were thwarted by political and theological issues in Graz; instead, Kepler applied for a job as a mathematician to Archduke Ferdinand in order to continue his astronomical studies. For this reason, Kepler wrote an article titled “In Terra inest virtus, quae Lunam ciet” (which is dedicated to Ferdinand) in which he put out a force-based explanation of lunar motion (“There is a force in the earth which causes the moon to move”).
He was not let into Ferdinand’s court despite the essay, but he did manage to apply a new technique he had developed for measuring lunar eclipses during the eclipse in Graz on July 10. His investigations into the laws of optics, which resulted in Astronomiae Pars Optica, were based on these findings.
Following their refusal to become Catholics, Kepler and his family were exiled from Graz on August 2, 1600. A few months later, Kepler went again to Prague, this time accompanied by his entire household. He had direct assistance from Tycho throughout the most of 1601, who gave him tasks including examining planetary observations and penning a pamphlet criticizing Tycho’s (by that point deceased) adversary, Ursus.
In September, Tycho was able to get him on board to work with him on the new project he had presented to the emperor: the Rudolphine Tables, which were intended to take the place of Erasmus Reinhold’s Prutenic Tables. Just two days after Tycho’s untimely death on October 24, 1601, Kepler was named the new imperial mathematician in charge, tasked with completing the unfinished business of his predecessor.
His most fruitful period as an imperial mathematician would last for the following eleven years.
Advisor Imperial
As the imperial mathematician, Kepler’s main duty was to advise the emperor on astrology. Even though Kepler was disapproving of modern astrologers’ attempts to accurately forecast the future or divine particular occurrences, he had been creating thorough horoscopes for friends, family, and clients since he was a student at Tübingen. When the emperor was having political problems, he went to Kepler for counsel in addition to horoscopes for foreign leaders and friends. Rudolf followed Kepler’s work in physical astronomy and had a keen interest in the work of many of his court academics, including several alchemists.
Officially, only Catholic and Utraquist theologies were recognized in Prague; nevertheless, Kepler’s standing in the imperial court permitted him to freely follow his Lutheran beliefs. Although the emperor was said to have given his family a substantial salary, it was always difficult to get enough money to pay commitments due to the overstretched imperial treasury. He and Barbara had a miserable home life filled with arguments and frequent illness, in part due to his financial difficulties. However, Kepler’s court career put him in touch with other eminent academics, like Johannes Brengger, Martin Bachazek, Jost Bürgi, David Fabricius, and Johannes Matthäus Wackher von Wackhenfels, and astronomical research advanced quickly.
The 1604 supernova

Kepler did not trust the tales about the appearance of a bright new evening star (SN 1604) until he saw it for himself in October of 1604. Kepler started tracking the supernova in a methodical manner. Astrologers predicted events of great portent, particularly pertaining to the emperor, because the end of 1603 signaled the beginning of a fiery trigon and the approximately 800-year cycle of great conjunctions. The two previous such periods were linked to the rise of Charlemagne (about 800 years earlier) and the birth of Christ (about 1600 years earlier).
Two years later, in his De Stella Nova, Kepler gave a description of the new star in this very context—that of the imperial mathematician and astrologer to the emperor. In it, Kepler discussed the astronomical characteristics of the star while expressing skepticism toward the several astrological interpretations that were popular at the time.
The concept of the immutability of the heavens—the belief held since Aristotle that the celestial spheres were flawless and unchanging—was further undermined by him as he observed its diminishing brightness, made assumptions about its origin, and claimed that it was in the sphere of fixed stars due to the absence of observed parallax. The variability of the sky was revealed by the birth of a new star.
Additionally, Kepler included an appendix in which he reviewed the recent chronology work of Polish historian Laurentius Suslyga. Based on his calculations, he determined that the Star of Bethlehem, which is comparable to the current new star, would have coincided with the first great conjunction of the previous 800-year cycle if Suslyga was correct in claiming that accepted timelines were four years behind.
In the next years, Kepler worked on chronology, particularly the date of events in Jesus’ life, and made an unsuccessful attempt to start a partnership with Italian astronomer Giovanni Antonio Magini. Kepler disseminated a draft of Somnium [The Dream], which would later be published (posthumously) in 1611. Somnium served as a demonstration of the viability of a non-geocentric system by describing astronomy from the viewpoint of a planet other than Earth. The text, which vanished after transferring hands several times, detailed an amazing journey to the Moon and was a combination of autobiography, allegory, and dissertation on interplanetary flight (often referred to as the first piece of science fiction).
Years later, a twisted version of the story—in which the narrator’s mother visits a demon to discover the techniques of space travel—may have sparked the witchcraft trial against his mother. After her final acquittal, Kepler wrote 223 footnotes to the narrative, many times longer than the text itself, explaining both the significant scientific information (especially about lunar geography) concealed in the story and its symbolic elements.
Later Years
Issues

The political-religious unrest in Prague reached a breaking point in 1611. Matthias, the brother of Emperor Rudolf, pushed the ill monarch to resign as King of Bohemia. Kepler took use of the fact that both sides sought his astrological assistance to offer accommodative political advice (with minimal relation to the stars, save for broad remarks against hasty action). Still, it was obvious that Kepler’s chances of survival in Matthias’ court were slim.
Barbara Kepler also developed Hungarian spotted fever that year, which led to her suffering seizures. Barbara was recuperating when all three of Kepler’s children had smallpox; Friedrich, age six, passed away. Kepler wrote to prospective donors in Württemberg and Padua after his son’s death.
Concerns over Kepler’s alleged Calvinist heresies at the University of Tübingen in Württemberg, which went against the Augsburg Confession and the Formula of Concord, kept him from returning. On the suggestion of the leaving Galileo, the University of Padua wanted to appoint Kepler as a mathematics professor. However, Kepler chose to remain in German territory and traveled to Austria in order to get a job as a teacher and district mathematician in Linz. However, shortly after Kepler’s return, Barbara fell ill again and passed away.
Kepler delayed moving to Linz and stayed in Prague until the early months of 1612 when Rudolf passed away. However, due to political turmoil, religious conflict, and familial sorrow (as well as the legal battle over his wife’s inheritance), Kepler was unable to do any study. Rather, he assembled a chronological text, Eclogae Chronicae, using prior research and communication. Kepler’s role (and pay) as the imperial mathematician was confirmed by Matthias, the succeeding Holy Roman Emperor, although he was permitted to relocate to Linz.
Linz (1612–1630)

Apart from finishing the Rudolphine Tables, Kepler’s main duties at Linz were teaching at the district school and offering astrological and astronomical services. Compared to his life in Prague, he had more financial stability and religious freedom during his early years there, despite his Lutheran church forbidding him from partaking in Communion due to his doctrinal reservations.
Kepler also had to cope with the charge of witchcraft against his mother Katharina in the Protestant town of Leonberg, as well as the subsequent ruling on the matter during his stay in Linz. That blow, which came just a few years after Kepler was excommunicated, is not considered a coincidence, but rather a sign of the full-scale attack that the Lutherans were waging on Kepler.
De vero Anno (1613), an extended thesis on the year of Christ’s birth, was his first publication in Linz. He also took part in discussions on whether Protestant Germany should adopt Pope Gregory’s revised calendar. Kepler married Susanna Reuttinger on October 30, 1613. Over a two-year period following the death of his first wife, Barbara, Kepler had evaluated 11 potential partners (a choice process that was subsequently codified as the marriage issue). After a while, he went back to Reuttinger (the sixth match), who he stated “won me over with love, humble loyalty, economy of household, diligence, and the love she gave the stepchildren.”
Kepler left for Regensburg on October 8, 1630, intending to get interest on work he had already completed. Kepler was unwell a few days after arriving in Regensburg, and his condition got worse. He passed away on November 15, 1630, a little more than a month after his arrival. He was laid to rest in a Protestant graveyard that the Thirty Years’ War entirely devastated.
Christianity
Kepler set out to discover and understand the principles governing the natural world, particularly those pertaining to astronomy since he believed that God had created the universe in an ordered manner. Although this is likely a condensed form of what he wrote by hand, the statement “I am merely thinking God’s thoughts after Him” has been attributed to him:
God intended for us to understand these principles of nature, which are within our reach, since he created us in his image, allowing us to participate in his ideas.
Kepler promoted religious tolerance, saying that Lutherans and Catholics ought to be allowed to partake in communion together, for example. He stated, “Christ the Lord neither was nor is Lutheran, nor Calvinist, nor Papist.”
Astronomy
Mysterium Cosmographicum

Mysterium Cosmographicum, or The Cosmographic Mystery, published in 1596, was Kepler’s first significant work in astronomy and the first published defense of the Copernican system. During a demonstration of the periodic conjunction of Saturn and Jupiter in the zodiac, Kepler claimed to have had an epiphany on July 19, 1595, while teaching in Graz. He realized that regular polygons bound one inscribed and one circumscribed circle at specific ratios, and he reasoned that this could be the geometrical basis of the universe. Kepler started working with 3-dimensional polyhedra when he was unable to locate a special arrangement of polygons that suited existing astronomical measurements (even when additional planets were added to the system).
He discovered that spherical spheres could be used to inscribe and circumscribe each of the five Platonic solids. By nesting these solids—each encased in a sphere—within one another, six layers were produced, representing the six planets that are currently known to exist: Mercury, Venus, Earth, Mars, Jupiter, and Saturn. Kepler discovered that, if the planets orbit the Sun, the spheres could be arranged at intervals that corresponded to the relative diameters of each planet’s route by carefully arranging the solids—octahedron, icosahedron, dodecahedron, tetrahedron, and cube.
Additionally, Kepler discovered a formula that connected the size of each planet’s orb to the duration of its orbital period: the ratio of orbital period increase from inner to outer planets is equal to twice the difference in orb radius.
Kepler eventually disapproved of this formula, though, as it lacked sufficient precision.
Kepler believed that the Mysterium had disclosed God’s universe-wide geometric design. Kepler’s theological beliefs regarding the relationship between the material and spiritual realms were a major source of his enthusiasm for the Copernican system. He believed that the universe was an image of God, with the Sun representing the Father, the star sphere representing the Son, and the space between them representing the Holy Spirit. An entire chapter in his initial draft of Mysterium attempted to reconcile biblical verses that appeared to support geocentrism with heliocentrism.
Kepler’s tutor, Michael Maestlin, helped him secure approval from the Tübingen university senate to publish his work. However, the publication of Kepler’s new ideas and a more streamlined, comprehensible explanation of the Copernican system were required before the Bible exegesis could be removed. Mysterium was not extensively read, but it solidified Kepler’s status as a highly accomplished astronomer. It was published late in 1596, and Kepler got his copies and started giving them to notable astronomers and benefactors early in 1597. The lavish dedication served as a vital gateway into the patronage system, both to influential benefactors and to the persons in charge of his position in Graz.
Mysterium was republished in 1621 in an extended version that was half as long as the original and included footnotes outlining the revisions and enhancements Kepler had made in the 25 years since the book’s initial release. Impact-wise, the Mysterium is a significant first step in modernizing Copernicus’ theory as presented in De revolutionibus orbium coelestium.
Mysterium Cosmographicum is largely responsible for modern astronomy, even with its main thesis flawed. “It represents the first step in cleansing the Copernican system of the remnants of the Ptolemaic theory still clinging to it,” says the author. “While Copernicus sought to advance a heliocentric system in this book, he resorted to Ptolemaic devices (viz., epicycles and eccentric circles) to explain the change in planets’ orbital speed. “As an aid to calculation and in order not to confuse the reader by diverging too much from Ptolemy.”
Astronomy in the Night

Under Tycho’s guidance, an extensive study program that resulted in Astronomia Nova (A New Astronomy)—which contained the first two laws of planetary motion—began with an examination of Mars’ orbit. In contrast to the widely accepted idea of a planetary orb—a spherical shell to which a planet is attached—Kepler presented the novel concept of a planetary orbit in this book, which is the route a planet takes in space as a consequence of physical reasons. This discovery led to the understanding that celestial phenomena are subject to physical principles.
Using an equant, a mathematical instrument that Copernicus had abolished with his method, Kepler computed and recalculated many estimates of Mars’s orbit until arriving at a model that, on average, coincided with Tycho’s measurements to within two arcminutes (the average measurement error). However, he was not happy with the intricate and somewhat off outcome; in some places, the model and data were out by as much as eight arcminutes. After using a variety of conventional mathematical astronomy techniques without success, Kepler attempted to fit an ovoid orbit to the data.
Kepler’s theological theory of the universe held that the Solar System’s driving force originated from the Sun, a representation of God the Father. Kepler used his own work on optics and William Gilbert’s conception of the Earth’s magnetic soul from De Magnete (1600) as analogies for his physical foundation. According to Kepler’s theory, planets move faster or slower in response to their distance from the Sun because the motive power, also known as the motive species, declines with distance. Maybe there was a mathematical link involved in this assumption that would bring astronomical order back.
In his formula, he established the inverse relationship between a planet’s distance from the Sun and its rate of motion, based on observations of the aphelion and perihelion of Earth and Mars. In order to streamline the process of verifying this connection throughout the course of the orbital cycle, Kepler restated the proportion in terms of geometry by late 1602, resulting in his second rule of planetary motion: planets sweep out equal areas in equal periods.
Using the geometrical rate law and the assumption of an egg-shaped ovoid orbit, he then set out to calculate Mars’ whole orbit. He made some forty unsuccessful efforts before, in late 1604, he finally came up with the concept of an ellipse, which he had previously thought would be too easy a solution for past astronomers to have missed. Kepler quickly came to the conclusion that all planets travel in ellipses, with the Sun at one focus, after seeing that an elliptical orbit (the Vicarious Hypothesis) suited the Mars data. This was his first law of planetary motion. He did not carry out the mathematical study beyond Mars since he did not have any calculating help.
He finished the Astronomia nova text by year’s end, but legal problems over Tycho’s observations—which belong to his heirs—would delay the book’s publication until 1609.
Epitome of Copernican Astronomy
Kepler had planned to write an astronomy textbook covering all the basics of heliocentric astronomy ever since finishing the Astronomia Nova. Over the following few years, Kepler worked on the project that would eventually become the Epitome of Copernican Astronomy or Epitome Astronomiae Copernicanae. The Epitome is more about Kepler’s own astronomical system than it is about the work of Copernicus, despite its title, which only alludes to heliocentrism. The Epitome tried to explain celestial motions by physical reasons and included all three laws of planetary motion.
It did not explain how elliptical orbits could be determined from observational data, even though it expressly extended the first two rules of planetary motion (applied to Mars in Astronomia nova) to all the planets, the Moon, and Jupiter’s Medean satellites[note 2].
Originally designed as a layman’s introduction, Kepler tried to emulate his mentor Michael Maestlin, who wrote a highly praised book that provided a general understanding of geocentric astronomy. Using Maestlin’s question-answer style, Kepler finished the first of three volumes (Books I–III) by 1615 and had it printed in 1617. However, the remaining two volumes would not be published until much later due to the Catholic Church’s ban on Copernican literature and the outbreak of the Thirty Years’ War.
As the arguments in The Epitome grew more complex and demanded a higher level of mathematics in order to understand, Kepler changed the book’s target audience from novices to astronomers and mathematicians in order to avoid being banned. Book IV of the second volume was released in 1620, while Books V–VII of the third volume were released in 1621.
Tables Rudolphine
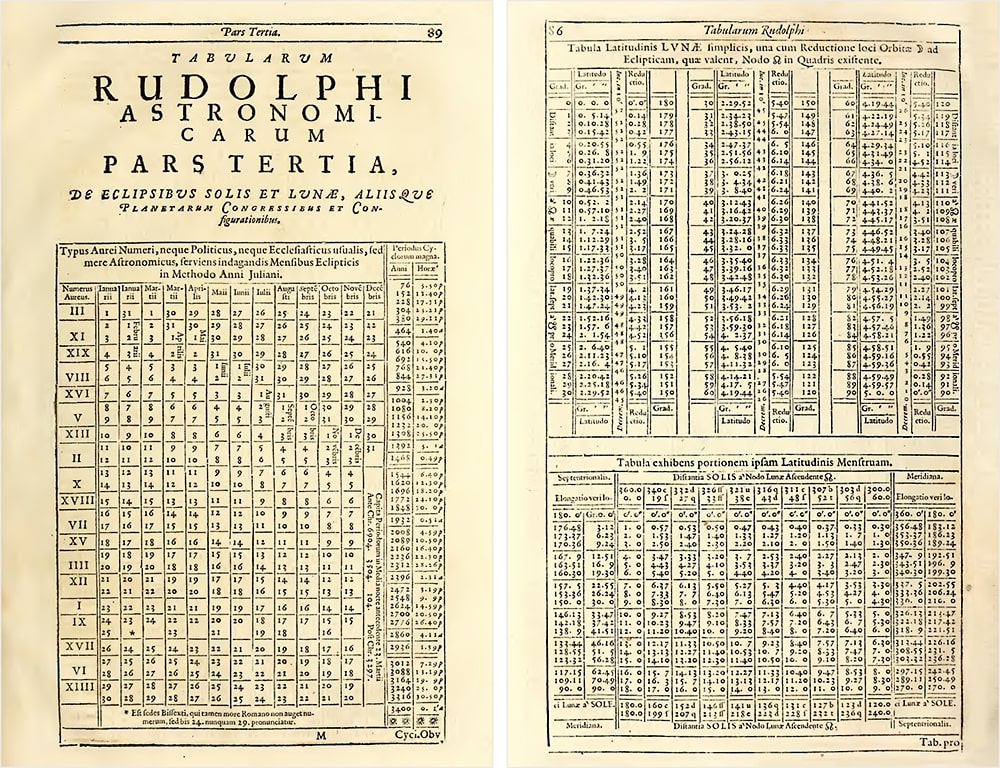
While none of these projects would be finished for many years, the majority of Kepler’s study in the years after Astronomia Nova was finished was devoted to the Rudolphine Tables and the creation of an extensive collection of ephemerides, or precise predictions of planet and star locations, based on the table.
The Rudolphine Tables, which were regarded as Kepler’s primary accomplishment at the time, were finally finished in 1623. But it wouldn’t be printed until 1627 because of the emperor’s publishing regulations and talks with Tycho Brahe’s successor.
Astrology
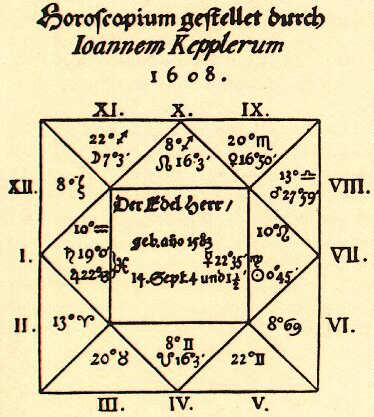
Kepler shared Ptolemy’s belief that astrology was the equivalent of astronomy in terms of interest and worth. But over the next several years, the two topics cooled down until professional astronomers stopped using astrology.
In his own day, Sir Oliver Lodge noted, Kepler was “continually attacking and throwing sarcasm at astrology, but it was the only thing for which people would pay him, and on it after a fashion, he lived,” suggesting a certain contempt for astrology. Still, Kepler devoted a great lot of effort to putting astrology back on a more solid intellectual foundation. He wrote a great deal about astrology itself, including several treatises, astrological calendars, and over 800 nativities.
De Fundamentis
As a brief preface to one of his annual almanacs, Kepler penned De Fundamentis (1601), whose full title translates as “On Giving Astrology Sounder Foundations,” as part of his ambition to become the imperial astronomer.
This book concludes with Kepler’s belief that the Earth has a soul with a sense of geometry. Kepler discusses the impact of the Sun, Moon, and planets upon humors in terms of their light. The world-soul, stimulated by the rays that create a geometric convergence around it, is sentient but not aware. Earth reacts to the angles and aspects created by the sky, but not consciously, any more than a shepherd enjoys the piping of a flute without knowing the principles of musical harmony. Eclipses are significant as omens because they induce a violent disturbance to the Earth’s animal faculty, which then experiences an emotion-like state and lasts for a while.
As an example, Kepler notes that “the highest tides of the sea are said by sailors to return after nineteen years around the same days of the year,” suggesting that the Earth has “cycles of humors” similar to those of live organisms. (The 18.6-year lunar node precession cycle may be referred to here.) Kepler suggests making a long-term collection of observations in order to look for such cycles, saying that “to date, this observation has not been made.”
Tertius Interveniens
Following the supernova of 1604, Kepler and Helisaeus Roeslin wrote a series of published critiques and rebuttals of each other’s arguments on the value of astrology; at the same time, physician Philip Feselius produced a book distancing astrology in general (and Roeslin’s work in particular).
Kepler composed Tertius Interveniens (1610) in reaction to what he perceived as the excesses of astrology on the one hand, and its ardent rejection on the other. This work, which was nominally presented to the common patron of Roeslin and Feselius, was intended to serve as an impartial mediator between the rivaling scholars (hence the term “Third-party interventions”).
However, it also outlined Kepler’s overall opinions about the usefulness of astrology, along with some theoretical explanations for the interactions between planets and specific souls. Although Kepler saw the majority of conventional astrological principles and practices as the “evil-smelling dung” that “an industrious hen” scoffs at, a diligent scientific astrologer may occasionally find an “occasional grain-seed, indeed, even a pearl or a gold nugget”.





