Antikythera mechanism

Hand-powered by Ancient Greeks, the Antikythera mechanism (/ˌaentɪkɪˈθɪərə/ AN-tik-ih-THEER-ʙ, US also /ˌæntaɪkɪˈ-/ AN-ty-kih-) is a replica of the solar system. It is the first instance of an analog computer that has been used to forecast eclipses and astronomical locations decades in advance. It might also be used to monitor the ancient Olympic Games’ four-year cycle, which is an Olympiad-like series of athletic competitions.

In 1901, wreckage from a shipwreck off the shore of the Greek island of Antikythera included this artifact. Archaeologist Valerios Stais determined that it included a gear in 1902. Housed within the remnants of a wooden-framed box of an approximate total size of 34 cm by 18 cm by 9 cm (13.4 in by 7.1 in by 3.5 in), the device was discovered as a single lump and subsequently broke into three main sections, which, following conservation efforts, are now fragmented into 82 individual shards. While several of these shards have inscriptions, four of them have gears. The biggest gear, which had 223 teeth initially, had a diameter of almost 13 cm (5 in).

All of these pieces of the mechanism, together with reproductions and reconstructions that show how it could have appeared and operated, are housed at the National Archaeological Museum in Athens.

Type:- Analogue computer
Writing:- Ancient Greek
Created:- 2nd century BC
Period/culture:- Hellenistic
Discovered:- 1901 Antikythera, Greece
Present location:- National Archaeological Museum, Athens

A Cardiff University team imaged inner pieces of the crust-encased mechanism in 2005 using computer X-ray tomography and high-resolution scanning, deciphering even the smallest inscriptions that had previously covered the outside casing. This implies that it had 37 bronze gears that meshed together to track the motions of the Sun and Moon across the zodiac, forecast eclipses, and simulate the Moon’s erratic orbit, in which the Moon travels faster at its apogee than at its perigee. Hipparchus of Rhodes, an astronomer, examined this motion in the second century BC, and it’s possible that he was involved in the machine’s design.

The five classical planets’ locations were determined by the technique, which may have some missing parts. In 2016, additional deciphering of the writings revealed numbers associated with Venus and Saturn’s synodic cycles.

The instrument has been variably dated to around 87 BC, between 150 and 100 BC, or 205 BC. It is thought to have been developed and built by Hellenistic scientists. It had to have been built prior to the shipwreck, which has been repeatedly dated to between 70 and 60 BC based on several lines of evidence. Researchers hypothesized in 2022 that the original calibration date—rather than the construction date—might have been December 23, 178 BC. A more plausible calibration date of 204 BC is suggested by some scientists. Similar complicated machines did not reappear in Western Europe until the fourteenth century.

Past Events

Finding out

The Antikythera wreck was found in early 1900 by Captain Dimitrios Kontos (Δημήτριος Κοvτός) and a group of sponge divers from Symi island. During the first voyage with the Hellenic Royal Navy, which took place in 1900–01, artifacts were retrieved. On the Greek island of Antikythera, the wreck of a Roman transport ship was discovered 45 meters (148 feet) below the surface at Point Glyphadia. Many huge things were recovered by the crew, such as money, jewelry, ceramics, unusual glassware, bronze and marble statues, and the mechanism. around 1901, perhaps around July, the mechanism was recovered from the debris. How the device ended up on the cargo ship is a mystery.

For storage and examination, every object recovered from the wreckage was moved to the National Museum of Archaeology in Athens. The mechanism looked like a lump of wood and tarnished bronze and was overlooked for two years as museum employees labored to piece together more visible artifacts, including the sculptures. Deformational alterations occurred because the mechanism was not handled after being removed from salt water.

Archaeologist Valerios Stais discovered a gear wheel lodged in one of the granite fragments on May 17, 1902. At first, he thought it was an astronomical clock, but most experts thought it was prochronistic, too intricate to have been built at the same time as the other components that had been found.

Albert Rehm, a German philologist, initially suggested that the instrument was an astronomical calculator after becoming intrigued by it.

The item was not investigated further until 1951 when Derek J. de Solla Price, a professor at Yale University and a British scientific historian, developed an interest in it. Price and Greek nuclear scientist Charalampos Karakalos scanned the 82 pieces using gamma and X-ray technology in 1971. In 1974, Price released a paper detailing their findings.

Artifacts and a second ship that could or might not be related to the treasure ship on which the mechanism was discovered were discovered during two more item searches conducted at the Antikythera wreck site in 2012 and 2015. A copper disc with a bull picture on it was also discovered. The disk was believed to have been a “cogwheel” that was a component of the Antikythera mechanism since it had four “ears” with holes in them. There doesn’t seem to be much proof that the disk was a component of the mechanism; it’s more probable that it was a bronze furniture ornament.

Origin

Most people agree that the Antikythera mechanism was the earliest known analog computer. The craftsmanship and intricacy of the mechanism’s construction imply that it has unidentified forebears back in the Hellenistic era. It is thought to have been erected in the late second or early first century BC, based on mathematical and astronomical ideas established by Greek astronomers around the second century BC.

Research conducted in 2008 by the Antikythera Mechanism Research Project indicated that the calendar on the Metonic Spiral was recognized as being from Corinth, or one of its colonies in northwest Greece or Sicily, indicating that the notion for the mechanism may have originated in the colonies.

The Antikythera Mechanism Research Project suggested in 2008 that it could suggest a relationship with the school of Archimedes, given Syracuse was the home of Archimedes and a colony of Corinth. In 2017, it was shown that the calendar on the Metonic Spiral is not the Syracuse calendar, but rather of the Corinthian kind.

According to a different idea, the device’s origin may have come from the ancient Greek city of Pergamon, which is home to the Library of Pergamum, and coins discovered by Jacques Cousteau at the wreck site in the 1970s date to the time of its creation. During the Hellenistic era, it was second only to the Library of Alexandria in prominence due to its numerous scrolls containing scientific and artistic works.

Vases in the Rhodian style were recovered aboard the ship that carried the device, suggesting that it was made at the academy that the Stoic philosopher Posidonius built on that Greek island. Hipparchus, the astronomer who lived at Rhodes from around 140 to 120 BC, was based there. Rhodes was a thriving commercial port, a hub for mechanical engineering, and an observatory.

Hipparchus may have invented, or at least worked on, the device, which employs his hypothesis of the Moon’s motion. The island of Rhodes is situated between latitudes 35.85 and 36.50 degrees north. It has been suggested that astronomical events on the Parapegma of the mechanism function best for latitudes in the range of 33.3–37.0 degrees north.

Based on the identification of the start-up date on the Saros Dial as the astronomical lunar month that commenced soon after the new moon of 28 April 205 BC, research published in 2014 argued for a revised date of about 200 BC. This idea states that the classic Greek trigonometric prediction style does not suit as well with the device’s predictive models as the Babylonian arithmetic approach.

According to a 2017 study by Iversen, the device’s prototype originated in Rhodes, but this specific model was customized for a customer from Epirus in northwest Greece. Iversen contends that the device was most likely built no earlier than a generation before the shipwreck, a claim that Jones (2017) supports.

In 2014 and 2015, more dives were conducted with the aim of learning more about the process. A new five-year session of the investigations began in May 2020 after the previous five-year program finished in October 2019. The investigations started in 2014.

Researchers hypothesized in 2022 that 23 December 178 BC could have been the mechanism’s initial calibration date—rather than its building date. A more plausible calibration date of 204 BC is suggested by some scientists. The astronomical clocks of Richard of Wallingford and Giovanni de’ Dondi are two early instances of machines of comparable complexity that did not reappear until the fourteenth century.

Design

It appears that the original mechanism was a single encrusted piece that came from the Mediterranean. Not very long after, it broke into three main halves. Some little fragments have fractured during cleaning and handling, while some were discovered by the Cousteau expedition on the ocean floor. It’s possible that other fragments are remained in storage, undetected since their first retrieval; Fragment F was found in this manner in 2005. Seven of the 82 known fragments are important mechanically and include most of the mechanism and inscriptions. Fractional and fragmentary inscriptions may be found on 16 other tiny components.

Major fragments

Fragment	Size [mm]	Weight [g]	Gears	Inscriptions	Notes
A	180 × 150	369.1	27	Yes	The main fragment contains the majority of the known mechanism. Clearly visible on the front is the large b1 gear, and under closer inspection further gears behind it (parts of the l, m, c, and d trains are visible as gears to the naked eye). The crank mechanism socket and the side-mounted gear that meshes with b1 is on Fragment A. The back of the fragment contains the rearmost e and k gears for synthesis of the moon anomaly, noticeable also is the pin and slot mechanism of the k train. It is noticed from detailed scans of the fragment that all gears are very closely packed and have sustained damage and displacement due to their years in the sea. The fragment is approximately 30 mm thick at its thickest point. Fragment A also contains divisions of the upper left quarter of the Saros spiral and 14 inscriptions from said spiral. The fragment also contains inscriptions for the exeligmos dial and visible on the back surface the remnants of the dial face. Finally, this fragment contains some back door inscriptions.
B	125 × 60	99.4	1	Yes	Contains approximately the bottom right third of the Metonic spiral and inscriptions of both the spiral and back door of the mechanism. The Metonic scale would have consisted of 235 cells of which 49 have been deciphered from fragment B either in whole or partially. The rest so far are assumed from knowledge of the Metonic cycle. This fragment also contains a single gear (o1) used in the Olympic train.
C	120 × 110	63.8	1	Yes	Contains parts of the upper right of the front dial face showing calendar and zodiac inscriptions. This fragment also contains the Moon indicator dial assembly including the Moon phase sphere in its housing and a single bevel gear (ma1) used in the Moon phase indication system.
D	45 × 35	15.0	1		Contains at least one unknown gear; according to Michael T. Wright it contains possibly two, and according to Xenophon Moussas it contains one gear (numbered 45 “ME”) inside a hollow gear giving the position of Jupiter reproducing it with epicyclic motion. Their purpose and position has not been ascertained to any accuracy or consensus, but lends to the debate for the possible planet displays on the face of the mechanism.
E	60 × 35	22.1		Yes	Found in 1976 and contains six inscriptions from the upper right of the Saros spiral.
F	90 × 80	86.2		Yes	Found in 2005 and contains 16 inscriptions from the lower right of the Saros spiral. It also contains remnants of the mechanism’s wooden housing.
G	125 × 110	31.7		Yes	A combination of fragments taken from fragment C while cleaning.

A tiny number of the smaller bits that have been discovered have writing on them, although most of them seem to be worthless. Important back door inscriptions can be found in Fragment 19, one of which reads, “… 76 years…” and alludes to the Callippic cycle. The back dials appear to have additional inscriptions that explain how they work. There are traces of inscriptions on fifteen more tiny fragments, in addition to this significant one.

Mechanics

The 2006 Nature article supplement by Freeth et al. has particular information about the data that were collected from the fragments.

Operation

The mechanism has a fixed ring dial with equal 30-degree sectors marking off the twelve zodiac signs, symbolizing the ecliptic. This corresponded with the Babylonian tradition of equitably allocating one-twelfth of the ecliptic to every sign of the zodiac, notwithstanding the irregular constellation borders.

There is another rotating ring outside that dial that is inscribed with the days and months of the Sothic Egyptian calendar—twelve months with thirty days each plus five intercalary days. The Egyptian names for the months that have been converted to Greek letters are used to identify the months. The Egyptian calendar ring must be rotated in order for the current zodiac points to line up. The Egyptian calendar progressed through a complete zodiac sign in around 120 years because it disregarded leap days.

The biggest gear, gear b1, which is the four-spoked gear seen on the front of fragment A, was connected to the mechanism by means of a crown gear, which was turned by a little hand crank that is now missing. As a result, the date indicator on the front dial was shifted to the appropriate day in the Egyptian calendar. Since most calendar cycles are not synchronous with the year, it is necessary to either look up the cycles indicated by the various calendar cycle indicators on the back in the Babylonian ephemeris tables for the day of the year currently set, since the year is not selectable.

If the mechanism were in good operating order, striking a certain day on the dial would be rather easy because the crank advances the date pointer around 78 days each full circle. When the hand crank was turned, all of the mechanism’s interlocking gears would revolve as well. This would allow the positions of the planets, the moon phase, eclipses, and calendar cycles to be calculated all at once.

The location of the spiral dial pointers on the two huge dials on the rear also needed to be known by the operator. The pointer had a “follower” that followed the metal spiral cuts as the dials featured four and five complete pointer revolutions. Before continuing, the pointer’s follower had to be physically transferred to the other end of the spiral whenever it reached the terminal month place at either end.

Faces

Front face

There are two concentric circular scales on the front dial. The Greek zodiac signs are indicated on the inner scale, which is divided into degrees. The outer scale is a moveable ring that runs in a channel and lies flush with the surface. It contains a series of holes in the channel under the ring that correspond to the number of days that are marked off on it.

This outer ring has been assumed to represent a 365-day Egyptian solar calendar since the mechanism was discovered more than a century ago. However, research (Budiselic, et al., 2020) challenged this assumption and provided direct statistical evidence that there are 354 intervals, suggesting a lunar calendar.

Since this original finding, the interval count has been independently determined by two study teams using distinct techniques. Using two separate approaches, Woan and Bayley compute 354–355 intervals, corroborating the findings of Budiselic et al. with more precision and stating that “365 holes is not plausible”.

The number of holes (N) “has to be integral and the SE (standard error) of 1.5 indicates that there is less than a 5% probability that N is not one of the six values in the range 350 to 355,” according to Malin and Dickens, who determined that the best estimate was 352.3±1.5. Less than one in ten thousand odds exist for N to be as high as 365. Of the two numbers that have been offered for N on astronomical grounds, Budiselic et al.’s value (354) is by far the most plausible, while alternative possibilities cannot be completely ruled out.”

Supporters of the 365-day hypothesis acknowledge that the mechanism predates the Julian calendar reform, but Ptolemy III’s attempted calendar reform in 238 BC shows that the Sothic and Callippic cycles had previously indicated a 365+1/4 day solar year. Although his planned leap day (Epag. 6) is not thought to be reflected in the dials, one may roll the scale back one day every four years by moving the outer calendar dial against the inner dial to account for the additional quarter-day in the solar year.

The most plausible explanation, assuming one accepts the 354-day data, is that the ring represents a 354-day lunar calendar. It may be the earliest instance of the Egyptian civil-based lunar calendar, as suggested by Richard Anthony Parker in 1950, given the period of the mechanism’s alleged creation and the Egyptian month names.

In addition to helping with the interpretation of the Metonic and Saros dials, the lunar calendar was intended to function as a daily indication of subsequent lunations. Unidentified gearing is suggested to drive a pointer around this scale by being synchronized with the remainder of the mechanism’s Metonic gearing. The ring’s movement and registration with respect to the underlying holes allowed for easy lunisolar intercalation and a 1-in-76-year correction to the Callippic cycle.

In addition, the dial indicates the Sun’s location on the ecliptic, which corresponds to the current year’s date. The ecliptic is a useful reference point for determining the locations of the Moon and the five planets that the Greeks were aware of, as their orbits are quite near to it.

The following three Egyptian months are inscribed in Greek letters on the surviving pieces of the outer ring:

• ΠΑΧΩΝ (Pachon)
• ΠΑΥΝΙ (Payne)
• ΕΠΙΦΙ (Epiphi)

Reconstructions of the other months have been made; however, some mechanisms have the Egyptian intercalary month’s five days left out. Greek inscriptions of the zodiac’s members may be found on the dial, which is said to be tailored to the tropical month form of the zodiac rather than the sidereal:

• ΢ΡΙΟΣ (Aries, Krios [Ram])
• ΤΑΥΡΟο (Bull of Taurus, Taurus)
• ΔΙΔΡΜΟΙ (Twins, Didymoi, Gemini)
• (Karkinos [Crab], Cancer)
• (Leon [Lion], Leo) ΫEΩΝ
• ΠΑΡΘΕΝΟΣ (Maiden, Parthenos), Virgo
• ΧΗΛΑΙ (Chelai, Libra, Zygos, or the Claw of Scorpio)
• (Skorpios [Scorpion], Scorpio) ΣΚΎΡΠΙΟΣ
• Sagittarius, Toxotes [Archer], ΧΎΞΎΧΗΣ
• ΑΙ΍ΟΚΕΡΩΣ (Aigokeros, Categorised as Goat-horned)
• ΥΔΡΟΧΟΟΣ (Aquarius, Hydrokhoos, water carrier)
• ΙΧΘΥΕΣ (Pisces, Ichthyes fish)

Rear face

The device not only followed the Metonic calendar and forecast solar eclipses, but it also computed the date of panhellenic sporting events, including the ancient Olympic Games, according to new results published in Nature in 2008. The names of the months on calendars from Epirus, a region in northwest Greece, and the island of Corfu, once known as Corcyra, roughly correspond with the inscriptions on the instrument.

The mechanism has five dials on its back: the two large displays, the Metonic and the Saros, and three smaller indicators, the Callippic, the exeligmos, and the so-called Olympiad Dial (now called the Games dial because it does not track Olympiad years, but rather the four-year cycle it tracks most closely, the Halieiad).

The primary top dial on the mechanism’s back is called the Metonic dial. The Metric cycle, measured in many physical units, is approximately equal to 235 synodic months, or less than 13 one-millionths of a tropical year. For this reason, it is a handy time span to switch between the solar and lunar calendars. The Metonic dial follows a spiral track with a follower on the pointer that monitors the spiral layer, covering 235 months in five dial revolutions. The Corinthian month names are contained in the cell, and the pointer points to the synodic month, which is calculated from new moon to new moon.

• Phoinikaios, or ΔOΙΝΙ΢ΑΙOΣ
• ΢ΡΑΝΕΙΎΣ (Kraneios)
• ΛΑΝΎΤΡΟΠΛΎΣ (Lanotropios)
• The term “mechanic” (ΜΑΧΑΝΕΥΣ) refers to Zeus the inventor.
• ΏΩؔΎ΢ΑΤΎΡΣ (Dodekateus)
• ΕΥ΢ΛΎΙΟΣ (Eukleios)
• ΑΡΤζΜΙοΙΟο (Artemisios)
• ΨΥΔΡΎΡΣ (Psydreus)
• Gameilios, ΓΑΜΕΙΛΙΟΣ
• ΑΓΡΙΑΝΙ��Σ (Agrianios)
• ΠΑΝؑ؜Οο (Panamos)
• Apellaios ΑΠΕΛΛΑΙΟΣ

With precision to within a week or so, setting the right solar time (in days) on the front panel thereby shows the current lunar month on the rear panel.

It has been suggested that the calendar on the mechanism is most likely the Epirote calendar, which was most likely adopted from a Corinthian colony in Epirus, possibly Ambracia, because the month names of the calendar match up with all the evidence of the Epirote calendar and the Games dial mentions the very minor Naa games of Dodona (in Epirus). Some have maintained that the calendar’s start date was immediately after the astronomical new moon of August 23, 205 BC and that the first month, Phoinikaios, was preferably the month in which the fall equinox fell.

The only pointer on the device that moves counter-clockwise as time passes is the Games dial, which is located as the right secondary top dial. The dial is divided into four sectors, each of which has the name of two Panhellenic Games, namely the Halieia of Rhodes and the Naa (held at Dodona), as well as a year indication. The “crown” games are Isthmia, Olympia, Nemea, and Pythia. The following are the inscriptions on each of the four divisions:

The primary lower spiral dial on the mechanism’s back is called the Saros dial. With a duration of 6585.333… days, the Saros cycle is 18 years and 11+1⁄3 days long, or extremely near to 223 synodic months (6585.3211 days). It might be used to forecast solar and lunar eclipses, not just the month but also the day and time of day since it is defined as the cycle of recurrence of the positions necessary to create them. Approximately eight hours more pass in a cycle than in an integer number of days. When expressed in terms of world spin, this indicates that an eclipse happens not just eight hours later but also one-third of a revolution to the west.

There are glyphs in 51 out of the 223 synodic month cells on the dial that indicate when 38 lunar and 27 solar eclipses will occur. Among the glyphs’ acronyms are the following:

• “Selene”, Moon; Σ = ΣΕΛΗ��Η
• (“Helios”, Sun) = ΗΛΙOΣ
• ΗΜ΅ΡΑο = H\M (“Hemeras”, for today)
• “Hours”, “hora” = “ωρα”
• N\Y is equal to “Nuktos” of the night.

The glyphs indicate the day, month, and hour of the eclipse, as well as whether it is a solar or lunar eclipse. Lunar eclipses can only be seen if the moon is above the horizon at the designated hour, while solar eclipses cannot be visible at all. Furthermore, the Saros dial’s inner lines at the cardinal points mark the beginning of a new full moon cycle. It has been suggested that the Saros dial began to operate soon after the astronomical new moon on April 28, 205 BC, based on the distribution of eclipse timings.

The secondary lower dial on the back of the mechanism is called the Exeligmos dial. The Exeligmos cycle is a triple Saros cycle that lasts for 54 years and 19,756 days. The full Exeligmos cycle returns the counting to an integral number of days, as indicated in the inscriptions, as the Saros cycle is to a third of a day, or 6,585 days + 8 hours. Its three divisions are labeled as follows:

Is it blank or o? (Assumedly, but not yet observed, indicating the number zero)
H (number 8) denotes an addition of 8 hours to the displayed time.
Iϻ (number 16) denotes adding 16 hours to the displayed time.

In order to get the precise eclipse timings, the dial pointer thus shows the number of hours that need to be added to the Saros dial’s glyph times.

Doors

The mechanism is housed in a wooden case that bears inscriptions on both the front and back doors. Seems to be the ‘instruction handbook’ through the back door. “76 years, 19 years” is engraved on one of its parts, signifying the Metonic and Callippic cycles. The Saros cycle’s “223” is also written. It is written “on the spiral subdivisions 235” on another portion of it, which alludes to the Metonic dial.

Putting in motion

The mechanism’s degree of miniaturization and component complexity, which is on par with astronomical clocks from the fourteenth century, make it noteworthy. It includes at least thirty gears, although Michael Wright, a specialist in mechanisms, suggests the Greeks of this era were able to devise a system with many more gears.

Whether the system had signs for each of the five planets that the ancient Greeks were aware of is a matter of controversy. All gears are present and accounted for, with the exception of one 63-toothed gear (r1) that is missing from fragment D. No gearing for such a planetary display exists.

Xenophon Moussas describes Fragment D as a tiny quasi-circular constriction with a gear inside a considerably bigger hollow gear. With the use of a pointer, the epicyclical motion produced by the inner gear moving within the outer gear may be used to determine Jupiter’s location. This little cylindrical box has two sides with the same number, 45, which is the Greek letter “ME” for the inner gear.

The front face served the function of positioning celestial bodies in relation to the celestial sphere along the ecliptic, taking into account the observer’s position on Earth. Whether the position was calculated from a geocentric or heliocentric perspective of the Solar System makes no difference; both computing approaches should provide the same position (ignoring ellipticity) within the mechanism’s error bounds.

Until Kepler (1571–1630) proposed the idea that orbits are ellipses, the epicyclic solar system of Ptolemy (c. 100–c. 170 AD), thousands of years after the mechanism’s apparent construction date, continued to advance with more epicycles and was more accurate in predicting planet positions than the Copernican view (1473–1543).

Evans et al. believe that just 17 more gears would be needed to display the mean positions of the five classical planets. These gears may be placed in front of the big driving gear and marked with separate circular dials on the face.

Planetary locations might be shown and the Sun anomaly could be synthesized with a version that used gear trains mechanically comparable to the lunar anomaly system, as modeled and reported by Freeth and Jones. They contend that their approach is more realistic than Wright’s model because it makes use of the Greeks’ well-known talents and avoids overly complicating or overstressing the machine internally.

With an average circular pitch of 1.6 mm, an average wheel thickness of 1.4 mm, and an average air space between gears of 1.2 mm, the gear teeth were equilateral triangles. The fact that some of the teeth do not even indicate that they were most likely made by hand from a blank metal ball.

Thanks to developments in imaging and X-ray technology, the size of the gears and the number of teeth inside the found shards can now be precisely determined. As a result, the device’s fundamental workings are now clear and have been faithfully recreated. The existence and kind of planet indicators continue to be the fundamental unanswered questions.

The gears, their teeth, and the predicted and calculated rotations of the significant gears are listed in the following table. The gear functions are derived from Freeth et al. (2008) and Freeth et al. (2012) for the lower part of the table. For the b1 gear, the computed numbers begin at one year per revolution, and the remaining values are calculated straight from the ratios of the gear teeth. The gears shown with an asterisk (*) have been computed with appropriate gear tooth counts, however, they are either absent from the known mechanism or their predecessors are missing. (Day lengths are computed based on the assumption that a year has 365.2425 days.)

Recognized gear arrangement

Given that the mechanism’s handbook mentions the intricate movements and periodicities of every planet, it is quite likely that planetary dials existed. We don’t know the precise location or workings of the planets’ gear systems. The Moon is the only place where a coaxial system exists. A planetary gear for Jupiter (Moussas, 2011, 2012, 2014) or a gear for the motion of the Sun (University of Thessaloniki group) is thought to be part of Fragment D, an epicycloidal system.

The big four-spoked mean Sun gear (b1) is driven by the hand crank that is attached to gear a1 and powers the Sun gear, which in turn powers the remaining gear sets. The Sun gear has 64 teeth on b2, which is b1/b2. It drives the date/mean sun pointer directly (the Freeth reconstruction discusses this in more detail below).

It’s possible that there was a second, “true sun” pointer that showed the Sun’s elliptical anomaly. This topic refers to the simulated rotational periods of different pointers and indicators; they are all based just on the gear ratios of the gears mentioned and are all predicated on the b1 gear’s 360-degree input rotation, or one tropical year.

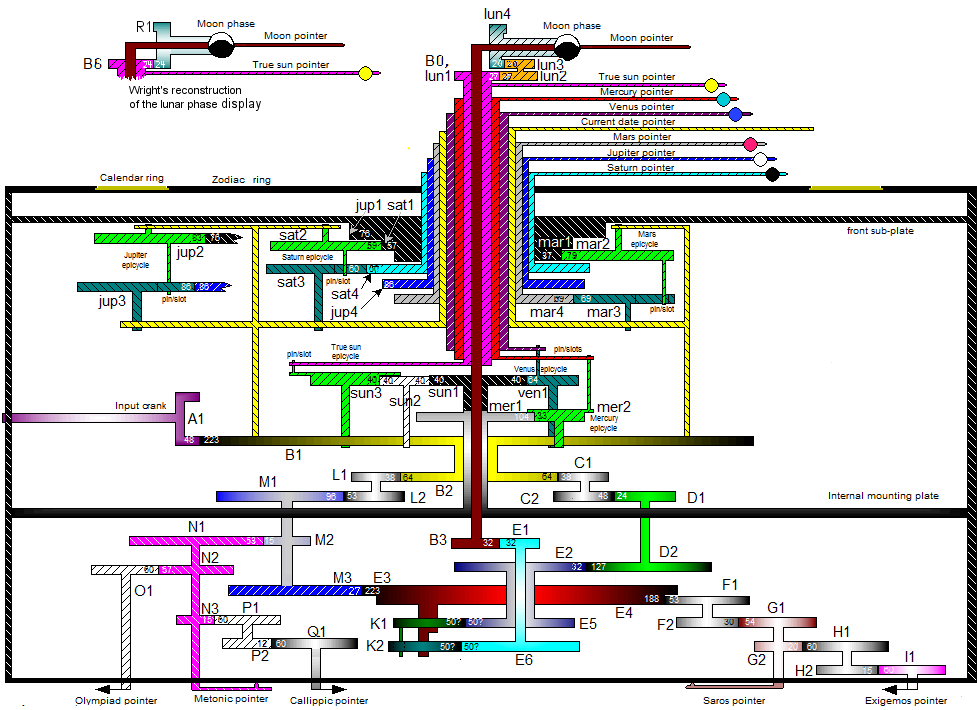
Gear b1 is the starting point of the Moon train, which continues via c1, c2, d1, d2, e2, e5, k1, k2, e6, e1, and b3 until it reaches the Moon pointer on the front face. The gears k1 and k2, which are identical pairs that function face-to-face instead of meshing, are combined to form an epicyclic gear system.

A short pin on k1 is placed into a slot in k2. The pin needs to travel back and forth in the slot because the two gears have different centers of rotation. As a result, the radius at which k2 is pushed changes, inevitably changing its angular velocity as well (assuming that k1’s velocity is even). This causes k2 to rotate more quickly in certain places than others.

The average velocities remain constant during a revolution, but Kepler’s second and third laws are modeled by the fast-slow variation, which accounts for the effects of the Moon’s elliptical orbit. The duration of a current lunar sidereal month is 27.321661 days, but the modeled rotational period of the Moon pointer (averaged over a year) is 27.321 days.

The k1/k2 gears are driven in a pin/slot configuration, which causes displacement to vary over a year. Mounting those two gears on the e3 gear provides a precessional advancement to the ellipticity modeling with a period of 8.8826 years, as opposed to the moon’s current precession period of 8.85 years.

The technique simulates the Moon’s phases as well. The Moon pointer has a shaft running the length of it, on which is fixed a small gear called r, which meshes to the Sun pointer at B0 (it is unclear from the original mechanism whether b0 is the actual date/mean Sun pointer or a hypothetical true Sun pointer because the connection between B0 and the rest of B is not visible).

The gear rotates at the synodic month period, effectively calculating the angle of the difference between the Sun and Moon pointers. It revolves around the dial in tandem with the Moon and is likewise oriented toward the Sun. A little ball that is painted half black and half white lengthwise and appears through a hole in the Moon pointer’s face to represent the phases visually is driven by the gear. The synodic month’s current value is 29.530589 days, while its simulated rotational period is 29.53 days.

The drive train b1, b2, l1, l2, m1, m2, and n1, which is attached to the pointer, powers the Metonic train. The pointer’s calculated rotating period spans 6939.5 days, representing the whole five-rotation spiral; in contrast, the Metonic cycle’s current value is 6939.69 days.

B1, B2, l1, l2, m1, m2, n1, n2, and o1, which mounts the pointer, are the ones driving the Olympiad train. As anticipated, its computed modeled rotational period is precisely four years. All the other pointers on the mechanism revolve in a clockwise direction, leaving just this one to spin counterclockwise.

Driven by b1, b2, l1, l2, m1, m2, n1, n3, p1, p2, and q1, which mounts the pointer, is the Callippic train. Its contemporary value is 27758.8 days, although its estimated simulated rotational period is 27758 days.

Driven by b1, b2, l1, l2, m1, m3, e3, e4, f1, f2, and g1, which mounts the pointer, is the Saros train. In four revolutions along the spiral pointer track, the Saros pointer’s rotating period of 1646.3 days is represented in the model; the current number is 1646.33 days.

Gears m3, n1-3, p1-2, and q1 do not seem to have survived the debris. The roles of the pointers were inferred from the remnants of the dials on the rear face, and a generally approved proposal for the acceptable, appropriate garage to carry out the functions was made.

Rebuilding initiatives

Proposed gear schemes

It is highly probable that the mechanism contained additional gearing that was either removed before being loaded onto the ship, lost in the shipwreck, or both because of the large space between the mean Sun gear and the front of the case, as well as the size and mechanical features of the mean Sun gear.

Numerous answers have been proposed over the years due to the absence of proof and the form of the mechanism’s front component, which has prompted efforts to mimic the actions of the Ancient Greeks. However, as efforts to read the inscriptions and analyze the interior architecture have advanced, older models have been discarded in favor of more accurate ones.

In the 1970s, Derek J. de Solla Price constructed a basic model.

Michael Wright created and constructed the first functional model in 2002 using the known mechanism and his simulation of a possible planetarium setup. He proposed that modifications would have been made for the deeper, more fundamental solar anomaly (referred to as the “first anomaly”) in addition to the lunar anomaly. Along with the known “mean sun” (the present time), he also provided pointers for the moon and this “true sun,” which includes Mercury, Venus, Mars, Jupiter, and Saturn.

A 2010 solution by Evans, Carman, and Thorndike differs significantly from Wright’s. Their suggestion was based on what they saw to be an off-center sun indication arrangement, which would simplify the mechanism by eliminating the requirement to replicate the solar anomaly.

They saw uneven spacing between the inscriptions on the front clock face. They proposed that simple dials for each planet would be used to indicate information such as major events in the planet’s cycle, first and last appearances in the night sky, and apparent direction changes, in place of accurate planetary indication, which was made impossible by the offset inscriptions. Compared to Wright’s concept, this method would result in a considerably simpler gear system with far less force and complexity.

They described the hitherto inexplicable 63 teeth gear in fragment D by using straightforward meshed gear trains. In response to criticism that they did not use the apparent fittings on the b1 gear, they offered two face plate layouts: one with dials placed uniformly apart and another with a gap at the top of the face. They suggested that the weather and seasonal iconography be shown via a window, in place of bearings and pillars, for the gears and axles. A method of epicyclic gearing with pin and slot followers was also proposed by Carman, Thorndike, and Evans in a 2012 publication.

In 2012, Freeth and Jones released a proposal. They put up a condensed and workable answer to the planetary indicator puzzle. Additionally, they suggest denoting the date on the month dial and the solar anomaly, or the sun’s apparent location in the zodiac dial, on a different pointer from the date pointer, which displays the sun’s mean position. The two dials’ front panel display is nearly identical to Wright’s if they are synchronized properly. In contrast to Wright’s model, this one is only a 3-D computer model and has not been physically constructed.

Three gears are used to synthesize the solar anomaly; the first is fixed in the center of the b1 gear and attached to the Sun spindle; the second is fixed on a spoke (in Wright’s proposal, the spoke on the bottom left) acting as an idle gear; and the final gear is positioned next to the first one. The final gear is equipped with an offset pin and, above said pin, an arm with a slot that is attached to the Sun spindle, causing anomaly as the mean Sun wheel rotates. This system is very similar to Wright’s proposal.

Venus, Mercury, and the Sun—which is considered a planet in this context—are all part of the inferior planet mechanism. Since the axis of each of the three systems’ epicyclic gears is placed on b1, the fundamental frequency of each system is the Earth year, as is really the case for all planets’ epicyclic motion, with the exception of the Sun. Every mesh has a gear that is grounded to the frame of the machine. In certain instances, the required distance between the gear’s center and the pin is more than the gear’s radius. Each has a pin installed, maybe on an extension of one side of the gear that enlarges the gear without interfering with the teeth.

In front of the front dials, a bar with a slot along the length of it runs from the pin toward the proper coaxial tube, the other end of which is the object pointer. The bars may have become whole gears, but because the slot is the sole functional component, there is no reason to waste metal. Additionally, by utilizing the bars, interference between the three mechanisms—each positioned on one of b1’s four spokes—is avoided.

Consequently, there are three epicyclic gears, three bars/coaxial tubes/pointers that would count as additional gears each, one new grounded gear (one was found in the wreckage, and the second is shared by two of the planets), one gear to reverse the direction of the sun anomaly, and a total of five gears and three slotted bars.

The fundamental idea of the lunar anomaly process is the same for the superior planet systems: Mars, Jupiter, and Saturn. Each has a gear that meshes with a grounded gear and whose center pivot is on an extension of b1, much like the inferior systems.

It displays a pin and the epicyclic gear’s center pivot, which includes a slot for the pin and meshes with a gear that is attached to a coaxial tube before connecting to the pointer. The three mechanisms are all on the same plane, parallel to the front dial plate, as each may be positioned inside a quadrant of the b1 extension. Each one makes use of a driving gear, driven gear, gear/coaxial tube/pointer, and ground gear, for a total of twelve extra gears.

To transfer the rotations in the mechanism to the eight-pointers, a total of eight coaxial spindles of varied nested sizes are used. Thus, the Freeth and Jones design has a total of 54 gears, three bars, and eight pointers—30 original gears, seven more gears added to complete calendar functionality, 17 gears, and three slotted bars to accommodate the six new pointers.

Small, spherical distinguishing stones adorn the pointers of the front zodiac dial in the illustration that Freeth gives. He makes reference to this passage from an old papyrus:

…a speaking voice approaches you. With the exception of the Sun and Moon, let the stars be arranged on the board according to [their] nature. And let the Sun be gold, the Moon be silver, the Gods be of (white?) stone, crystalline (?) Ares [Mars] of reddish onyx, Aphrodite [Venus] of lapis lazuli veined with gold, Hermes [Mercury] of turquoise, and Kronos [Saturn] of obsidian.

Nevertheless, more recent findings and investigations have demonstrated that the aforementioned models are incorrect. In computed tomography scans of the inscriptions pertaining to Venus and Saturn, respectively, the numerals 462 and 442 were discovered in 2016. These correspond to these planets’ synodic cycles and show that the process was more precise than previously believed. The Antikythera Mechanism Research Project suggested modifications to the gearing and created mechanical components in 2018 based on the CT scans.

A new suggested reconstruction of the full Antikythera Mechanism was released in March 2021 by the University College London Antikythera Research Team, under the direction of Freeth. Using logical estimates for the synodic cycles, which have modest prime factors—factors 7 and 17 are utilized for more than one planet—they were able to identify gears that could be shared throughout the gear trains for the several planets.

They come to the conclusion that while their model is compatible with the data now available, none of the earlier models “are at all compatible with all the currently known data”. A movie narrated by Freeth explains the findings of the mechanism’s operation as well as the identification of the synodic cycle times.

Precision

Freeth and Jones’ investigations show that their simulated mechanism is erroneous. There are times when the Mars pointer is up to 38° off. These errors happen around the nodal points of Mars’ retrograde motion, and they get smaller at other places in the orbit. This is caused by shortcomings in the Greek idea of planetary motions rather than errors in the gearing ratios inside the mechanism. It was not possible to increase the precision until Ptolemy published his Almagest in 160 AD, especially when he included the idea of the equant into his theory. Kepler’s equations of planetary motion were introduced much later, in 1609 and 1619.

The Antikythera Mechanism, one of the great wonders of antiquity, was, in essence, a machine built to forecast celestial phenomena in accordance with the advanced astronomical theories of the time. It is the only evidence of a lost history of brilliant engineering and a concept of pure genius. However, it wasn’t very effective!

Apart from theoretical precision, mechanical accuracy is another concern. Freeth and Jones observe that the finer solar and lunar correction mechanisms put into the mechanism would have likely been overwhelmed by the inherent “looseness” in the mechanism caused by the hand-made gears with their triangular teeth and the frictions between gears and in bearing surfaces:

Even though the engineering was impressive for the time, new research shows that the design concept was far more precise than the engineering precision used in its manufacture. This led to significant cumulative errors in the gear trains, which would have eliminated many of the subtle anomalies in the design.

The hand-made triangular teeth may have contributed to the device’s inaccuracies, but the technology and calculations used to create the elliptical paths of the planets and the retrograde motion of the Moon and Mars—which included a clockwork-style gear train with a pin-and-slot epicyclic mechanism—predated the first known clocks discovered in antiquity in medieval Europe by more than a millennium.

The approximate value of pi, the notion of centers of gravity, and the steps Archimedes took to establish calculus imply the Greeks had a sufficient understanding of mathematics beyond Babylonian algebra to simulate the elliptical character of planetary motion.

The Moon mechanism, which is especially fascinating to physicists, indicates the moon’s location and phase using a unique train of bronze gears, two of which are connected by a slightly off-center axis. The moon circles the Earth at different speeds, as we know from Kepler’s equations of planetary motion. The Antikythera Mechanism models this speed difference, even though the Ancient Greeks were unaware of the orbit’s true elliptical form.

Comparable literary techniques from antiquity

The mechanism’s degree of sophistication suggests that the device was not unique and may have required knowledge accumulated over many generations. These artifacts, however, were rarely preserved to the current day and were frequently melted down for the bronze’s worth.

Roman world

Cicero cites two devices in his De re publica (55–51 BC), a philosophical conversation from the first century BC, that some contemporary writers believe to be a planetarium or orrery that predicted the motions of the Sun, Moon, and the five planets that were known at the time. Following Archimedes’ demise at the siege of Syracuse in 212 BC, the Roman commander Marcus Claudius Marcellus took both of them to Rome. Marcellus held Archimedes in high regard, and the sole artifact he retained from the siege was one of these devices (the other was stored in the Temple of Virtue).

The device was preserved as a family heirloom, and according to Cicero, Gaius Sulpicius Gallus (consul with Marcellus’s nephew in 166 BC, and credited by Pliny the Elder as the first Roman to have written a book explaining solar and lunar eclipses) gave both a “learned explanation” and a working demonstration of the device. Philus was one of the participants in a conversation that Cicero imagined had taken place in a villa belonging to Scipio Aemilianus in the year 129 BC.

I had heard a lot about this heavenly globe or sphere because of Archimedes’s renown. On the other hand, I didn’t find its appearance all that remarkable. Another, more refined in shape and widely recognized, was molded by the same Archimedes and placed in the Rome Temple of Virtue by Marcellus. However, as soon as Gallus started to describe the construction of this machine using his amazing science, I had the impression that the Sicilian geometrician was a genius above everything we would typically consider to be a part of our nature.

Gallus reassured us that the solid and compact globe was a very old innovation, with Thales of Miletus having shown the original model. Later, Eudoxus of Cnidus, a disciple of Plato, drew the stars that appear in the sky on its surface, and many years later, Aratus illustrated them in his poems using poetic description instead of any scientific science, after stealing Eudoxus’ exquisite design and representation. He continued by saying that the early solid globe was unable to depict the figure of the sphere, which showed the movements of the Sun, Moon, and five planets, or wandering stars.

And that’s where Archimedes’ creativity shone, for he’d worked out how one revolution should sustain varied and uneven progressions in different movements. The link between the Moon and the Sun was depicted when Gallus rotated this globe, and the bronze device’s number of spins matched the number of days on the actual sky globe accurately. As a result, it depicted both the Moon passing through the region of the Earth’s shadow while the Sun is in line and the same eclipse of the Sun as seen on the globe [of the sky].

According to Pappus of Alexandria (c. 290–350 AD), Archimedes penned a lost treatise titled “On Sphere-Making” that described how to make these devices. Many of his innovations are described in the ancient manuscripts that have survived, some of which even have basic drawings.

His odometer is one such instrument; it is the same kind that the Romans used to set their mile markers (as reported by Vitruvius, Heron of Alexandria, and during the reign of Emperor Commodus). While the text’s pictures seemed to work, attempts to construct them exactly as they were shown had failed. The contraption worked well when the square-toothed gears in the illustration were swapped out for angled gears similar to those in the Antikythera mechanism.

If the history written by Cicero is accurate, this technique dates back to the third century BC. Later Roman authors including Lactantius (Divinarum Institutionum Libri VII), Claudian (In spheres Archimedes), and Proclus (Commentary on the first book of Euclid’s Elements of Geometry) in the fourth and fifth centuries also make reference to Archimedes’ invention.

Cicero said that another similar instrument, “… each of the revolutions of which brings about the same movement in the Sun and Moon and five wandering stars [planets] as is brought about each day and night in the heavens,” was constructed “recently” by his friend Posidonius.

Given that the three devices were almost certainly in Posidonius’ hands by the time the shipwreck was estimated to have occurred, and that both the devices made by Archimedes and Cicero were located in Rome at least thirty years after the shipwreck, it is unlikely that any one of these machines was the Antikythera mechanism discovered in the wreck. The Antikythera mechanism was too complex to have been a singular device, according to the experts who have recreated it.

Eastern Mediterranean, among other regions

The notion that there was a Greek tradition of sophisticated mechanical technology that was subsequently, at least in part, transmitted to the Byzantine and Islamic worlds, where sophisticated, albeit simpler, mechanical devices were constructed during the Middle Ages, is supported by the evidence that the Antikythera mechanism was not unique.

There are fragments of a geared calendar from the fifth or sixth-century Byzantine Empire that were affixed to a sundial; it is possible that the calendar served as a tool for timekeeping. The Caliph of Baghdad ordered Banū Mūsā’s Kitab al-Hiyal, also known as the Book of Ingenious Devices, in the early ninth century AD.

More than a hundred mechanical devices were mentioned in this literature, some of which could have originated from Greek manuscripts that have been kept in monasteries. Around 1000, the scholar al-Biruni described a geared calendar that resembled the Byzantine mechanism. Additionally, a clockwork device resembling the Byzantine device may be found in a surviving 13th-century astrolabe. There is a chance that this medieval technology made its way to Europe and influenced the creation of mechanical clocks there.

The Chinese scholar Su Song built a mechanical clock tower in the eleventh century that, among other things, could tell the positions of some stars and planets on an armillary sphere that was mechanically rotated.

Replicas in museums and popular culture

Prior to the major “Antikythera shipwreck” display at the National Archaeological Museum in Athens, a number of exhibitions have been held across the world. In 2012, the Antikythera mechanism was on display with restorations by Ioannis Theofanidis, Derek de Solla Price, Michael Wright, the Thessaloniki University, and Dionysios Kriaris as part of a temporary exhibition about the Antikythera shipwreck.

Additional replicas may be seen in the Children’s Museum of Manhattan in New York, the American Computer Museum in Bozeman, Montana, the Astronomisch-Physikalisches Kabinett in Kassel, Germany, the Archimedes Museum in Olympia, Greece, and the Musée des Arts et Métiers in Paris.

An episode named “Star Clock BC” from the National Geographic documentary series Naked Science was devoted to the Antikythera Mechanism and broadcast on January 20, 2011. In 2012, Tony Freeth, a researcher on Antikythera mechanisms, made a documentary titled The World’s First Computer.

The Two-Thousand-Year-Old Computer debuted on BBC Four in 2012 and was rerun as Ancient Computer on NOVA, the PBS science series, on April 3, 2013, in the United States. It details the mechanism’s discovery and the Antikythera Mechanism Research Project’s 2005 research on it.

A working Lego replica of the Antikythera mechanism was constructed by enthusiast Andy Carol in 2010 and was used in a 2011 short film made by Small Mammal.

Google released a Google Doodle on May 17, 2017, to commemorate the discovery’s 115th anniversary.

The building of a reproduction of an Antikythera mechanism utilizing tools, metallurgical and machining processes, and materials that would have been accessible in ancient Greece is documented on the YouTube channel Clickspring. Additionally, the video explores the potential technology of the time.

A fictitious version of the mechanism—also known as Archimedes’ Dial, the title Dial of Destiny—is the central theme of the 2023 movie Indiana Jones and the Dial of Destiny. According to the movie, Archimedes created the gadget as a temporal mapping system, but a former Nazi scientist wanted to use it as a means of time travel to help Germany win World War II.

A 10X scale copy of the device was constructed, set up, and officially opened at the University of Sonora in Hermosillo, Sonora, Mexico on February 8, 2024. Dr. Alfonso conducted the inauguration under the name Monumental Antikythera Mechanism for Hermosillo (MAMH). The Governor of Sonora, Durazo Montaño, the Chancellor of the Universidad de Sonora, Dr. Maria Rita Plancarte Martinez, the Greek Ambassador, Nikolaos Koutrokois, and a group from the Embassy were also present.

Here are 50 detailed facts about the Antikythera Mechanism:

1. What It Is: The Antikythera Mechanism is an ancient Greek analog device used to predict astronomical positions and eclipses, often considered the world’s first computer.
2. Discovery: The device was discovered in 1901 by sponge divers near the Greek island of Antikythera, among the remains of a Roman-era shipwreck.
3. Age: The mechanism is believed to have been created between 150 and 100 BC, making it over 2,000 years old.
4. Materials: The Antikythera Mechanism is made primarily of bronze gears housed in a wooden frame, although only fragments of the wood remain today.
5. Complexity: It consists of more than 30 interlocking bronze gears, which is an incredibly complex engineering feat for its time.
6. Purpose: The mechanism was used to calculate and display the positions of celestial bodies, including the Sun, Moon, and planets, as well as predict solar and lunar eclipses.
7. Gear Ratio: The gears inside the mechanism have a precise gear ratio, allowing for complex calculations of astronomical cycles, such as the Metonic cycle (a 19-year cycle relating to lunar and solar years).
8. First Multigear Device: It is the oldest known device to use multiple gears in such an intricate manner, showcasing ancient Greek expertise in mathematics and engineering.
9. Metonic Cycle: The device tracks the Metonic cycle, which harmonizes the solar year with the lunar year every 19 years, ensuring the synchronization of lunar and solar calendars.
10. Saros Cycle: It also includes the Saros cycle, an 18-year period used to predict eclipses, still used in modern eclipse prediction.
11. Zodiac and Calendar: The front of the mechanism features a Zodiac dial and a calendar dial, showing the months and positions of celestial bodies according to the ancient Greek calendar.
12. Planetary Motions: Researchers believe the mechanism also modeled the movements of the five known planets at the time: Mercury, Venus, Mars, Jupiter, and Saturn.
13. Sophisticated Engineering: The Antikythera Mechanism’s engineering is so sophisticated that it took modern technology years to understand its full function. It was far ahead of its time in mechanical design.
14. Antikythera Shipwreck: The mechanism was discovered in the remains of a Roman cargo ship that sank around 60 BC, carrying various Greek treasures.
15. Location: The mechanism is currently housed in the National Archaeological Museum in Athens, Greece, where it is one of the most prized artifacts.
16. Inscription: The mechanism includes numerous ancient Greek inscriptions, which helped archaeologists and researchers understand its use and operation.
17. Gearing Technology: The intricate gear systems in the mechanism are so advanced that it was not until the 14th century AD that similarly complex gearing mechanisms appeared in Europe.
18. Lunar Phases: The device could track the phases of the Moon, showing its waxing and waning cycles, calculated with great precision.
19. Eclipse Prediction: The mechanism could predict both solar and lunar eclipses, providing the exact dates and times based on the Saros cycle.
20. Epicyclic Gearing: The device uses epicyclic gearing, where gears rotate around other gears, a complex engineering feature also seen in modern planetary gear systems.
21. Corroded Fragments: The device was discovered in 82 heavily corroded fragments, which were pieced together over decades of study.
22. Advanced Astronomy: The Antikythera Mechanism showcases the advanced knowledge of astronomy that ancient Greeks possessed, especially in modeling celestial phenomena.
23. Lost Knowledge: The mechanism represents a lost era of Greek mechanical engineering that was not documented in texts and was far more advanced than previously known.
24. No Other Examples: There are no other known devices from the ancient world that approach the complexity of the Antikythera Mechanism.
25. X-ray Analysis: Modern researchers have used X-ray and CT scanning to peer inside the corroded fragments of the device and reconstruct its gears and dials.
26. Reconstruction Efforts: Several working replicas of the Antikythera Mechanism have been built, based on the information gleaned from the original fragments.
27. Planetary Hypotheses: While the device tracks planetary movements, it assumes a geocentric model of the universe, with Earth at the center, as was common in ancient Greek astronomy.
28. Cicero’s Mention: Roman philosopher Cicero wrote about similar devices created by ancient Greek mathematician Archimedes, suggesting that such mechanisms were known to scholars at the time.
29. Planetary Theory: The mechanism incorporates ancient Greek theories of planetary motion, particularly using epicycles to explain retrograde motions of planets.
30. Front and Back Dials: The device had two main displays: a front dial for solar and lunar cycles and a back dial for eclipse predictions.
31. Precession of the Equinoxes: It is believed that the mechanism also accounted for the precession of the equinoxes, a gradual shift in the orientation of Earth’s rotational axis.
32. Moon’s Anomaly: The device compensates for the Moon’s variable speed in its orbit, a level of precision that surprised modern engineers and scientists.
33. Cultural Importance: The Antikythera Mechanism is often viewed as one of the greatest treasures of ancient Greek culture, reflecting their advanced understanding of both mechanics and astronomy.
34. The Missing Link: The Antikythera Mechanism is sometimes referred to as the “missing link” in the history of mechanical technology, bridging the gap between ancient and modern machines.
35. Archimedes’ Influence: Some scholars speculate that the mechanism may have been influenced by the work of Archimedes, though this is not confirmed.
36. Mechanism’s Origin: It is widely believed that the Antikythera Mechanism was created in the Hellenistic period, likely in Rhodes, a known center of mechanical engineering at the time.
37. Ancient Astronomers: The device reflects the work of Hipparchus, a Greek astronomer who developed a detailed model of lunar and solar movements.
38. Roman Connection: While the mechanism itself is Greek, it was discovered in a Roman shipwreck, showing that the Romans valued and transported Greek technology.
39. Navigation: Some researchers theorize that the mechanism may have been used in navigation, although this theory is debated.
40. Gears Per Revolution: The gears in the mechanism are finely crafted to achieve different numbers of revolutions per year for the Sun, Moon, and planets, based on ancient astronomical models.
41. Engineering Marvel: The device is considered an engineering marvel, so advanced that many modern scientists found it difficult to believe it could have been built with ancient technology.
42. Shipwreck Context: The shipwreck from which the mechanism was recovered also contained luxury items, indicating that it may have belonged to a wealthy individual or even a scholar.
43. Hypothetical Creator: Some historians believe the Antikythera Mechanism was constructed by Geminos of Rhodes, a mathematician and astronomer from the Hellenistic era.
44. Planets on the Mechanism: The five known planets at the time—Mercury, Venus, Mars, Jupiter, and Saturn—are believed to have been represented by rotating dials on the mechanism.
45. Functionality Lost: Much of the mechanism’s functionality remains lost due to the damage it sustained over centuries underwater and the incomplete state of its fragments.
46. Global Impact: The discovery of the Antikythera Mechanism had a profound impact on our understanding of ancient science, changing views on the level of technological sophistication in the ancient world.
47. Timekeeping: The mechanism likely functioned as a calendar, tracking both the solar year and important Greek cycles, such as Olympic cycles and religious festivals.
48. Astronomical Calendars: The dials on the mechanism were capable of representing different astronomical calendars in use in the Hellenistic world, possibly even including Egyptian and Babylonian systems.
49. No Known Predecessors: There are no known earlier devices with comparable complexity, making the Antikythera Mechanism a unique artifact in the history of technology.
50. Philosophical Implications: The Antikythera Mechanism also reflects the Greek philosophical tradition, where the heavens were seen as a system of order and harmony, capable of being modeled and understood through mathematics and mechanics.

Like1